Energy in SHM

The equation of motion for pendulum is

The displacement of a particle of mass $m$ performing SHM with amplitude $A$ and angular frequency $\omega$ is given by

$x=A\cos \left(\omega t\right)$

Derive an equation of kinetic energy for this particle in terms of time.

The potential energy of a particle performing SHM is given by $U=\frac{1}{2}k{A}^2{\sin }^2\left(\omega t\right)$. Which one of the following options correctly represents the graph for potential energy vs. time?

A particle of mass $m$ oscillates in Simple Harmonic Motion between points $x_1$ and $x_2$, the equilibrium position being $O$. Which of the following graphs represents the variation of its potential energy $\left(U\right)$ with respect to its position?

A block of mass $\mathrm{M}$ is placed on a smooth horizontal surface, and it is pulled by a light spring as shown in the diagram. If the ends $\mathrm{A}$ and $\mathrm{B}$ of the spring are moving with $4 \mathrm{m} {\mathrm{s}}^{-1}$ and $2 \mathrm{m} {\mathrm{s}}^{-1}$ respectively in the same direction and at this moment the rate at which spring energy is increasing is $20 \mathrm{J} {\mathrm{s}}^{-1}$, then what is the value of spring force (in $\mathrm{N}$)?

If the inertial mass and gravitational mass of the simple pendulum of length $l$ are not equal, then the time period of the simple pendulum is

When a spring is stretched by $10 \mathrm{cm}$, the potential energy stored is $E$. When the spring is stretched by $10 \mathrm{cm}$ more, the potential energy stored in the spring becomes

A mass of $0.2 \mathrm{kg}$ is attached to the lower end of a massless spring of force constant $200 \mathrm{N} {\mathrm{m}}^{-1}$, the upper end of which is fixed to a rigid support. Which of the following statement is true?

$U$ is the potential energy of an oscillating(SHM) particle and $F$ is the force acting on it at a given instant. Which of the following is correct?

(Given $x$ is displacement of the particle)

In case of a simple pendulum, time period versus length is depicted by

The potential energy of a simple harmonic oscillator of mass $2 \mathrm{kg}$ at its mean position is $5 \mathrm{J}$. If its total energy is $9 \mathrm{J}$ and amplitude is $1 \mathrm{cm}$, then its time period is

A force constant of ideal spring is $200 \mathrm{N} {\mathrm{m}}^{-1}$. It is loaded with a mass $\frac{200}{{\pi }^2} \mathrm{kg}$ at the lower end the period of its vibration is:

The $KE$ and $PE$ of a particle executing simple harmonic motion with amplitude $A$ has ratio $2:1$, then its displacement is,

A particle is executing $\mathrm{SHM}$  with time period $T\mathit{ }$. Starting from mean position, time taken by it to complete $\frac{5}{8}$ oscillations, is

A disc of radius $R$ and mass $M$ is pivoted at the rim about an axis which is perpendicular to its plane and its set for small oscillations. If the simple pendulum has to have the same period as that of the disc, then find the value of four times the length (in meter) of the simple pendulum if $R=\frac{1}{2} m$.

Angular frequency in SHM is given by $\text{ω}=\sqrt{\frac{\text{k}}{\text{m}}}$. Maximum acceleration in SHM is ${\text{ω}}^{2}A$ and maximum value of friction between two bodies in contact is $\text{μ}\text{N}$, where N is the normal reaction between the bodies.
  Now the value of k, the force constant is increased, then the maximum amplitude calculated in above question will

Electrostatic force on a charged particle is given by $\overrightarrow{\text{F}}=\text{q}\overrightarrow{\text{E}}$. If q is positive $\overrightarrow{\text{F}}\uparrow \uparrow \overrightarrow{\text{E}}$ and if q negative $\overrightarrow{\text{F}}\uparrow \downarrow \overrightarrow{\text{E}}$

In the figure m_A = m_B = 1 kg. Block A is neutral while q_B = - 1C. Sizes of A and B are negligible. B is released from rest at a distance 1.8 m from A. Initially  spring is neither compressed nor elongated.

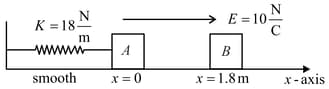
Equilibrium position of the combined mass is at $x = ........m$

A simple pendulum of length $L$ has mass $M$ and it oscillates freely with amplitude $A$. At extreme position, its potential energy is ($g$= acceleration due to gravity)

A simple pendulum is suspended from the ceiling of a stationary lift. Its time period is measured as $T$. If the lift accelerates upward its time period will be 

At the instant speed of block is maximum, the magnitude of force exerted by spring on the block is: